Research - Sudipta Hensh

Research Overview

I study some of the most fascinating and extreme phenomena in the universe through the lens of multi-messenger astrophysics—combining signals from gravitational waves, electromagnetic radiation to uncover the physics of cosmic events. My focus is on compact objects such as black holes, neutron stars, which push matter and spacetime to their limits. These objects are powerful laboratories for testing the laws of physics, from the nature of gravity to the behavior of matter at ultra-high densities. Using a combination of theoretical models and computational simulations, I explore how these systems form, evolve, and produce the signals we can detect on Earth. My work aims to connect the underlying physics with observations, helping us better understand the universe and the fundamental forces that shape it. Below, you’ll find detailed information about my current and previous research efforts. Enthusiasts are encouraged to follow along in what follows.

Gravitational Waveform Modeling

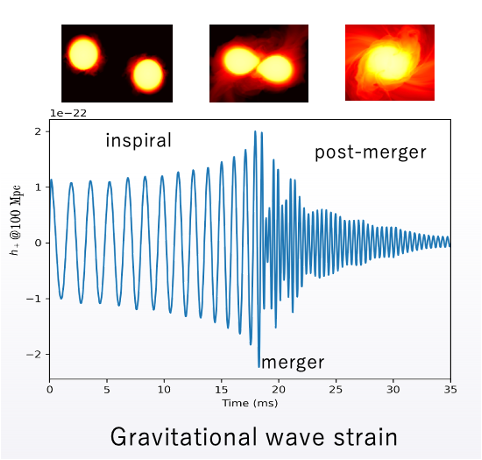
Gravitational waves are tiny ripples in the fabric of spacetime, set off by some of the most cataclysmic events in the Universe—such as the collision of two black holes, the merger of neutron stars, the merger of a neutron star and a black hole, or the explosion of a massive star in a supernova. In a binary merger, two compact objects spiral closer and closer together, dancing around each other in a cosmic waltz before finally colliding to form a single, even more massive object.

As these massive bodies move through spacetime, they create distortions that radiate outward at the speed of light—gravitational waves. Albert Einstein first predicted their existence about a century ago, shortly after developing his general theory of relativity. For decades, they remained a purely theoretical concept—until 2015, when the LIGO/Virgo/KAGRA collaboration made the first direct detection. Since then, many more events have been observed, including the famous binary neutron star merger of 2017, which provided a treasure trove of information and confirmed key predictions of physics.

To predict and detect gravitational waves, scientists need accurate “waveform templates” in advance. These templates are compared against data from detectors to identify real signals buried in noise. Early in a merger, gravitational waves can be modeled with high accuracy using post-Newtonian approximations. But as the objects approach each other and enter the violent merger phase, the problem becomes too complex for simple equations—requiring full-blown numerical relativity, where the coupled, nonlinear Einstein field equations are solved on powerful supercomputers.

My research focuses on enriching these waveform template banks by exploring a wide range of binary system parameters. This work is crucial for the next generation of detections, as advanced ground-based observatories like LIGO and future space missions such as LISA will capture more—and more varied—events. Beyond simply detecting these waves, they give us a unique way to probe gravity itself.

Binary neutron star mergers

Binary Neutron Stars Mergers

Neutron stars are among the densest objects in the Universe—so dense that a teaspoon of their matter would weigh billions of tons. When two neutron stars collide, the event is nothing short of extraordinary: they unleash gravitational waves, produce bursts of high-energy gamma rays, and bring all four fundamental forces of nature—gravity, electromagnetism, and the strong and weak nuclear forces—into play at once.

These mergers are also thought to be cosmic factories for some of the heaviest elements in the Universe. The origin of elements like gold, platinum, and uranium is still not fully understood, but one leading explanation is rapid neutron capture, or r-process nucleosynthesis. In a neutron star merger, the extreme densities and temperatures of the neutron-rich environment provide the ideal conditions for the r-process to occur. The newly formed r-process elements undergo radioactive decay, producing a glow known as a kilonova—a phenomenon spectacularly confirmed in the 2017 observation of the binary neutron star merger GW170817. Neutron stars themselves are often embedded in incredibly strong magnetic fields, and during a merger, these fields can help launch tightly focused jets of gamma rays across vast cosmic distances. Yet, despite all these observations, much about neutron star interiors remains a mystery—especially how pressure changes with density at the ultra-high densities found in their cores. Such conditions cannot be reproduced in terrestrial laboratories, making these mergers an invaluable natural laboratory for testing nuclear physics, gravity, and astrophysics in their most extreme forms. The physics of neutron star mergers is enormously complex, involving the interplay of relativistic hydrodynamics, gravity, and radiation transport. My research focuses on the high-density part of the nuclear equation of state—the relationship between pressure, density, and temperature deep inside neutron stars. At sufficiently high densities, matter is expected to undergo a transition into a deconfined quark phase. In this state, hadrons such as protons and neutrons no longer exist as bound particles; instead, their constituents — quarks and gluons — form a new state of matter known as quark–gluon plasma.

In this direction of research, I performed numerical relativity simulations using quark–hadron crossover equations of state to study how these exotic forms of matter affect the gravitational wave signal, particularly the post-merger peak frequency. This offers a potential way to distinguish different equations of state directly from future gravitational wave observations. In this way, neutron star mergers serve as cosmic laboratories—places where the laws of physics are pushed to their limits. Each new detection is not just an astronomical event, but a rare opportunity to probe the deep structure of matter, test our theories of gravity in the strongest possible fields, and uncover the origins of the elements that shape our world. As gravitational wave astronomy advances, we stand on the threshold of discoveries that could transform our understanding of the Universe at its most fundamental level.

Properties of spacetime with torsion

"If history had been reversed and the spin of the electron discovered before 1915, I have little doubt that Einstein would have wanted to include torsion in his original formulation of General Relativity."
— Dennis W. Sciama, 1979

A general notion of spacetime is as described by Einstein’s general relativity—a smooth fabric that bends and curves in response to matter and energy. But there’s another possibility: spacetime might also possess torsion, a kind of “twist” in its geometry in addition to curvature. While curvature tells matter how to move, torsion could, in principle, couple to an intrinsic property of matter called spin—a quantum feature of elementary particles. Extending Einstein’s general relativity incorporating particles intrinsic spin was done by Sciama and Kibble independently in 1960, which is known as Einstein-Cartan theory of gravity. However, this is a class of theories of gravity with torsion, not the only theory with torsion.

Raychaudhuri equations, a set of equations for the evolution of expansion, shear, and vorticity, describe how congruence moves in a spacetime. A remarkable feature of these equations is that they are purely geometrical and does not consider a theory of gravity a priori. Raychauri equations is a cornerstone of the Hawking-Penrose singularity theorem. In our work, I explored how torsion could affect some of the most fundamental aspects of gravity. I worked on generalization of the Raychaudhuri equations to include the effects of torsion. These extended equations are fully geometrical like the original Raychaudhuri equations. We revisitied the gravitational collapse of pressureless dust in Einstein-Cartan theory using modified Raychaudhuri equations with torsion. It is found that with non-zero torsion, the null energy condition can be violated before collapsing matter reaches Planck density—suggesting a potential way for nature to avoid the formation of singularities.

I also investigated how torsion could influence the behavior of black holes, finding significant modifications to the tidal heating process and the spectrum of Hawking radiation. Together, these studies suggest that torsion—if present in nature—could shape the fate of collapsing matter and leave imprints on signals we might one day observe.

Image of black hole-keplerian disk system

Raytracing around black hole

Light moves along straight line in flat spacetime. However, in a curved spacetime, it follows the curvature of the spacetime. According to classical general relativity, Black hole is black, meaning nothing can be seen coming out of the black hole including lights. Black holes accrete matter from their surroundings as material loses angular momentum and falls inward under gravity. If the black hole is surrounded by an accretion disk-matter distribution around black holes, not all the radiation i.e. photons falling into the black hole will be captured. It can be captured, it can be lost in the space- meaning never reaching to us, it can come directly to us, or it can make a short trip around the black hole before reaching to us. Short trip means it may orbit the black hole once or multiple times before escaping to reach us. These winding paths produce what are called higher-order images, faint additional rings surrounding the main image of the accretion disk. Thanks to the curve geometry, accretion disk radiation received in our telescopes can give us an idea about the optical appearance of a black hole.

In 2019, the Event Horizon Telescope (EHT) — a network of telescopes captured the first real image of a black hole. Raytracing is a technique used to simulate how light travels near black holes. EHT relies heavily on general relativistic raytracing simulations for to compare the interferometric data of real observations, by first simulating the system and then comparing the results with the actual images. I have contributed to developing a ray-tracing code. A demonstration of the image of the black hole surrounded by the Novikov-Thorne thin disk using our raytracing simulation is on the right of the text. Our method uses backward raytracing, where we start from the observer’s point of view and trace light rays backward to find their origins. I have also used raytracing to explore how light might appear if gravity behaves differently from what Einstein’s theory predicts. These studies help test the limits of our understanding of gravity.

With future upgrades to the EHT and new telescopes coming online, we expect to see black holes in even greater detail. Raytracing will remain essential for interpreting these incredible observations.

Gravitational Lensing

Gravitational lensing is one of the most fascinating predictions of Einstein’s theory of relativity. When light from a distant star or galaxy passes near a massive object, such as a black hole or a cluster of galaxies, the light does not travel in a straight line. Instead, it bends along the curved fabric of spacetime, much like the path of light through a glass lens. This bending can stretch, distort, or even multiply the image of the distant source. For astronomers, this effect has become an invaluable tool: it reveals the presence of otherwise invisible matter, helps trace the distribution of dark matter in the universe, and even provides ways to measure cosmic expansion. While general relativity has explained lensing with great success, scientists are still searching for a more complete picture of gravity that also works hand in hand with quantum mechanics. One candidate theory is called Hořava–Lifshitz gravity.

My research explored what happens when light travels near compact objects—like black holes—within this modified theory of gravity, especially when the black hole is surrounded by plasma. Plasma is a thin, ionized gas that naturally exists around such extreme environments, and it affects how light moves. Depending on whether the plasma is uniform or unevenly spread out, it can either reduce or increase the amount of bending. These effects don’t just change the path of light—they also alter what we would actually see. The size and shape of the dark “shadow” cast by a black hole can shift, and the brightness of the lensed images can change. In particular, if the plasma is clumpy or distributed unevenly, the magnification of a lensed image can become much stronger, contrary to the uniform distribution of plasma in which case the magnification decreases. This means the object being lensed could appear significantly brighter or fainter than it would in empty space.

Taken together, these results suggest that both the nature of gravity itself and the properties of the surrounding plasma leave clear signatures on gravitational lensing. Future high-resolution observations of black holes and other strong lensing systems may be able to detect these differences. By carefully comparing theory with what we see in the sky, we can test whether Einstein’s description of gravity remains complete—or if new physics is waiting to be discovered.